Lecture 10 Real-time Physically-based Materials (surface models)

PBR and PBR Materials 基于物理渲染的材质

PBR = Physically-Based Rendering 基于物理的渲染

任何渲染都可以是基于物理
材质、光照、相机、光线传播等等
不只是限制在材质范围内，但是指的往往是材质

在RTR中的PBR材质

RTR中使用的材质要远少于在offline中的材质
RTR中说是基于物理的，但实际上并不是基于物理
分两类，基本上和离线渲染差不多，但是更多着眼于技巧来提升速度
1. 表面材质（微表面模型、迪士尼原则BRDFs Hyperion）
2. 对体积（非表面模型）来说，头发、云、皮肤等，大多都是着眼于快速和近似的方法实现单散射和多次散射

这里复习了一下材质的BRDF，这里面包含：

菲涅尔项
NDF 法线分布函数，有很多类
- Beckmann NDF 形式上很像高斯正态分布，各向同性的结果（也能异性），其中 $\alpha$表示粗糙程度，$\theta_h$表示入射与出射角的半矢量h与法线的夹角。
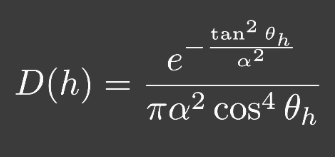
- GGX(TR) NDF 特点“long tail”，在大角度的时候相对于beckmann有更大的值，看起来beckmann高光比较尖锐，GGX更柔和一点，看起来更自然一点。
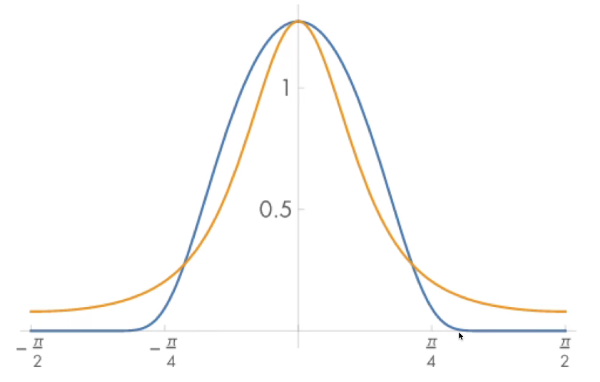
- GTR ,GGX的增强版，添加一项$\gamma$，2的时候是TR，很大的时候是趋向于Beckmann。
Shadowing-Masking Term（或者说叫Geometry Term）
- 为了表示出微表面的自遮挡现象
- shadowing：光线的遮挡。 masking：视野的遮挡
- 一般拆分成两部分——光线遮挡和视野遮挡
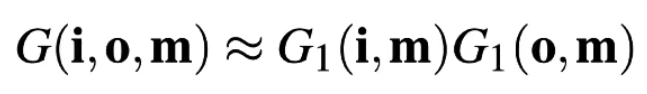
- 提供一个遮挡项，让其在很锐利的角度（Grazing Angle）的时候变得更暗，在靠近90度的时候剧烈变暗
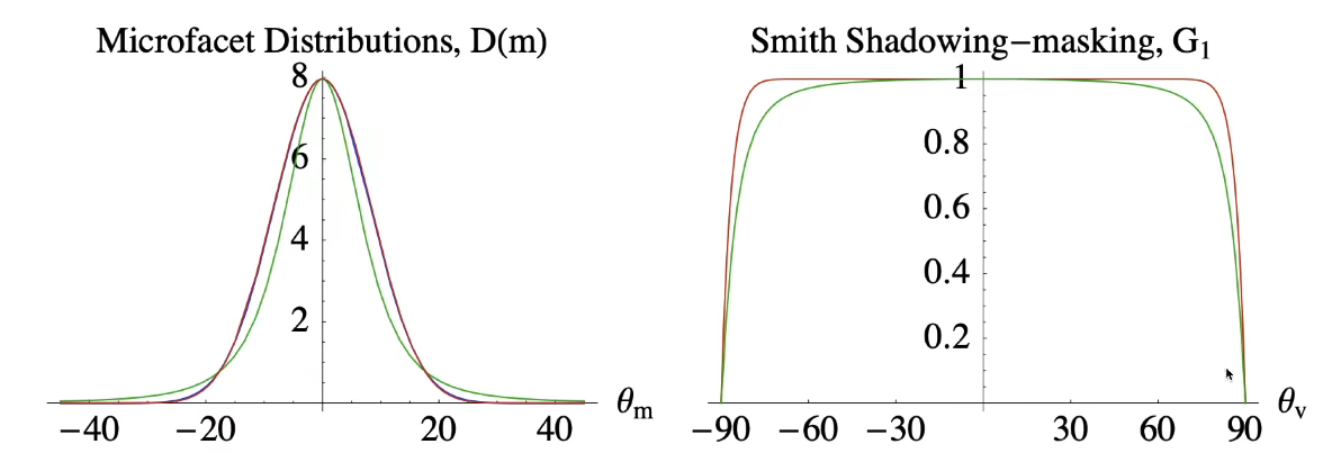
- 造成的问题：丢失了能量。越粗糙的表面，能量在表面中多次弹射的占比就越大。使用G项会让整体的能量损失。（测试方法叫做White Furnace Test 白炉测试）
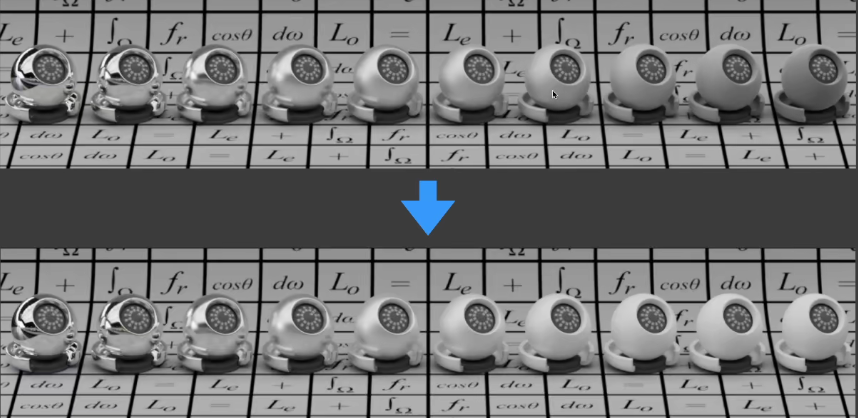
  - 解决：The Kulla-Conty Approximation
  - 从2D的BRDF lobe中的能量中算出实际射出的能量E，1-E就是损失能量
  - 为了补充这部分，就给原BRDF增加一项
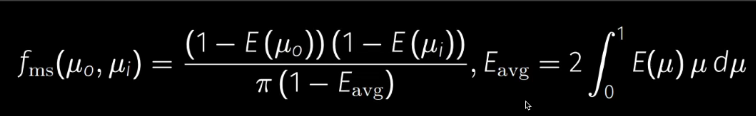
  - 之所以用$\frac{(1-E(\mu_0))(1-E(\mu_i))}{\pi(1-E_{avg})}$这种形式，是考虑到光路可逆的这个”对称性“。这种形式积分就能得到1-E。加上他就能能量守恒了。
  - $E_{avg}$是常数。但是算$E_{avg}$太难了，但是可以使用之前学过的split sum思想进行”预计算“（或者说打表），如此加快运算速度。
- 如果BRDF有颜色的话(多次弹射BRDF)：
  - 颜色就是吸收，就是能量损失，所以我们只需要考虑能量损失，就是考虑颜色
- 定义一个平均菲涅尔项，表示反射出去的能量
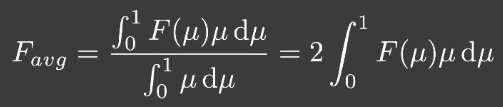
- 能直接看到的部分：$E_{avg}F_{avg}$
- 一次反弹之后能看到的部分：$F_{avg}(1-E_{avg})\cdot F_{avg}E_{avg}$
- k次反弹之后能看到的部分：$F_{avg}^k(1-E_{avg})^k\cdot F_{avg}E_{avg}$
- $k\longrightarrow\infty$, 得到总的energy term：$\frac{F_{avg}E_{avg}}{1-F_{avg}(1-E_{avg})}$