Physics-Based Ray Tracing
Physics-Based Ray Tracing
Ray-Triangle Intersection
有很多关于光线和三角形求交的算法,这里学习一下包含三角形的参数平面重心坐标算法,因为它不包含除了三角形顶点的长期存储。
为了将一个光线和参数平面求交,我们设置了一个笛卡尔坐标方程组:
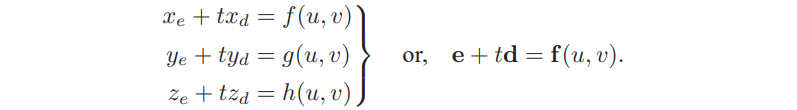
等号左边是光线经过了多少t和三角形相交,右边是光线和三角形交点坐标在三角形参数平面上的uv坐标。
在参数平面上,所有点都是abc三个点的线性组合,也就是说:
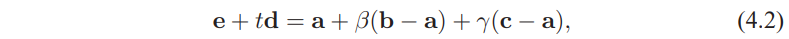
其中beta和gamma需要当且仅当$\beta>0,\ \gamma>0,\ \beta+\gamma<1$时,交点才在三角形上。从上面的方程可以得到关于t,beta,gamma的方程组:
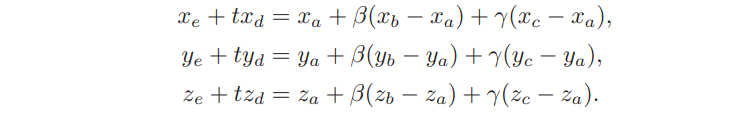
易转换为线性系统:
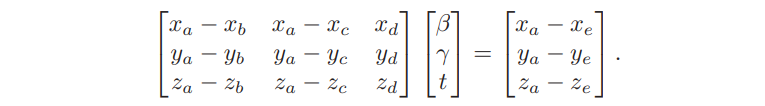
经典的算法是用克拉默法则(Cramer’s Rule)嗯算。这里貌似也只讲了克拉默法则嗯算,算出t,beta和gamma。
最后程序的结果是这样


不过为啥我看的shader里面的求交算的比这个麻烦很多,因为涉及到很多数值计算上的细节。
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Chuan 川 Charles!
评论



