读 BI-DIRECTIONAL PATH TRACING 论文
BI-DIRECTIONAL PATH TRACING 双向路径追踪
图形学研究进展需要复现一篇SIGGRAPH,遂找了一篇网上还没代码的论文。这里学习一下其基础:双向路径追踪。
Abstract
在本文中,我们提出了一种新的蒙特卡罗渲染算法,该算法无缝集成了拍摄和采集能力,以创建真实感图像。该算法可以被解释为众所周知的路径跟踪算法的推广。测试结果表明,它在间接照明很重要的典型室内场景中表现得更好。
Introduction
作者提出了一种新的蒙特卡洛算法来将光源和眼睛顶点放在相同的基础上处理,此之谓双向路径追踪。
后面提到了一篇多pass的渲染论文,问了下chatgpt:
《A progressive multi-pass method for global illumination》是一篇关于全局照明的论文。该论文提出了一种渐进式多通道方法,用于解决全局照明中的光照计算问题。
该方法基于迭代的思想,通过多次迭代来逐步优化全局照明的计算结果。具体来说,该方法分为多个通道,每个通道都对应着一种光照计算模型,例如光线跟踪、辐射度传输、环境光照等。在每个通道中,该方法会使用之前通道的计算结果作为输入,然后进行局部光照计算,得到新的局部光照贡献,并将其累加到全局光照中。
通过这种渐进式的多通道方法,该论文提出的算法能够在保证光照计算精度的前提下,大大提高计算效率。同时,该方法还具有较好的可扩展性和灵活性,可以根据具体应用场景进行灵活的调整和优化。
总之,《A progressive multi-pass method for global illumination》是一篇针对全局照明计算问题的重要研究成果,对于提高计算效率和优化光照渲染效果具有重要的实际意义。
RELATED WORK
基于辐射原理的方法是在计算机图形学中全局光照理论中的一个重要里程碑,主要是定义了一系列光能量的传递规律。这种方法是不依赖于视角的,因为是从光源出发,看有多少能打到我的视角像素。此后Kajiya提出了渲染方程并引入了路径追踪作为一种蒙特卡罗方法来算这个方程。这个想法就是去采样通过像素的光通量,通过路径追踪到光源把光集中起来。这种方法是视角依赖的。蒙特卡洛可以解决大部分这类问题,但是收敛起来很慢。($\sqrt{N}$速度)
目前大多数全局光照的问题都是指向2-pass方法的,就是说先计算diffuse部分,再算一个pass计算specular的光的部分。diffuse部分用一种确定性的方法计算,或者用一种蒙特卡罗方法。包括specular反射的最终图像通常使用一些分布式光线追踪或者路径追踪的变体。一些算法是同重建不仅diffuse的部分,而且还有发射出的光的有向(directional)部分,从而找到一种完全不依赖于视角的方法。主要问题在于后面的这种方法要大量的存储来表达光照函数。
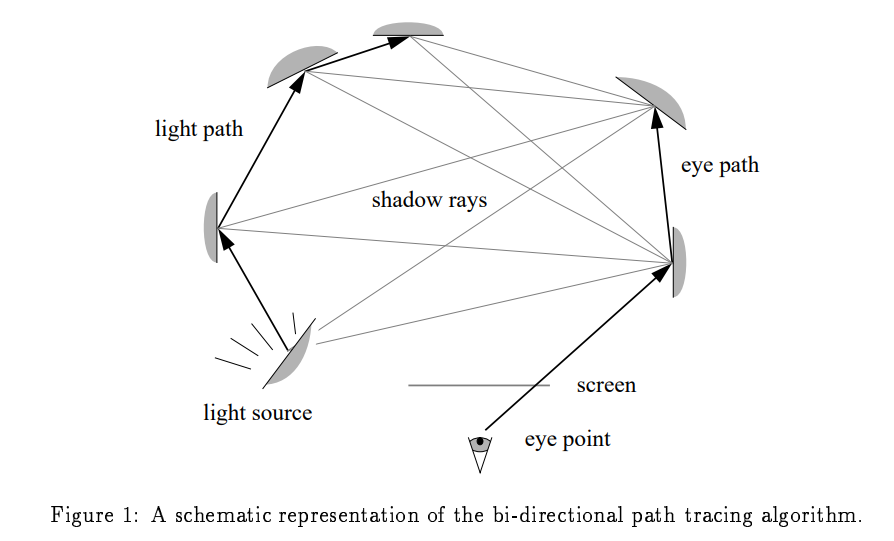
Bi-directional Path Tracing
我们展示的算法不同于分布光线追踪或者是路径追踪。主要思想是。物体同时,以相同的方式,被选择的光顶点与视角顶点照到。所有的在视角路径上的hit point都会用shadow ray来连接,不只解决直接光源,还有二级、三级等照射的可能路线。
Performing the random walks
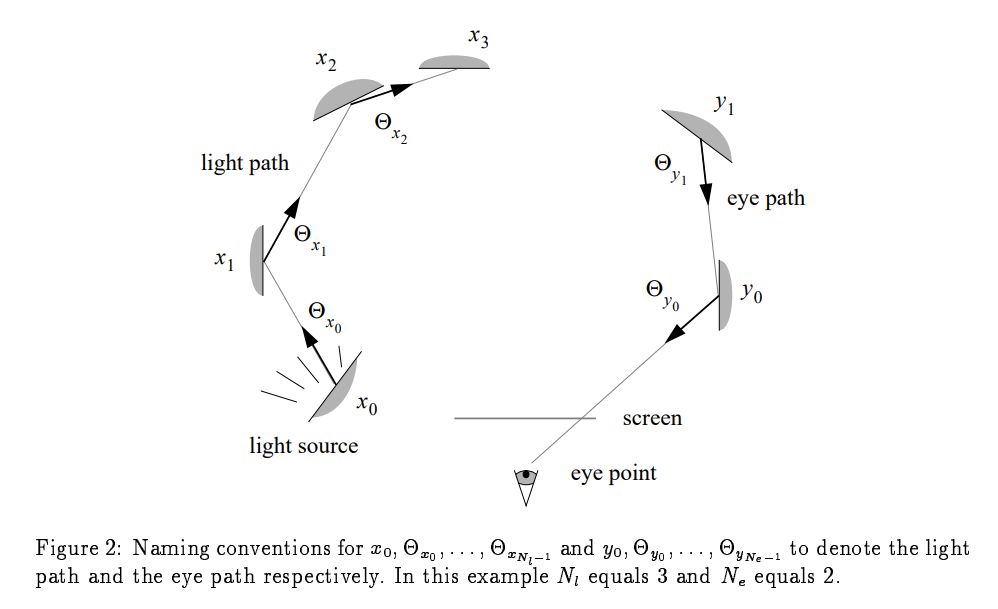
之后是如何生成路径的问题。$x_0$到$x_{N_l}$生成光顶点,$y_0$到$y_{Ne}$是视角顶点。
对于光顶点,生成$x_0$和$\Theta_{x_0}$:
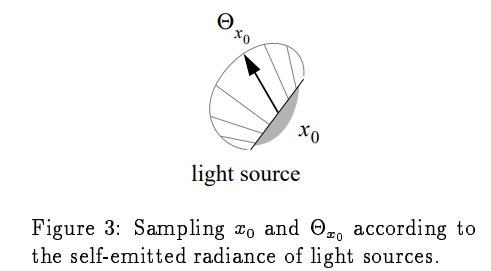
使用重要性采样,在概率密度函数大的地方,被采到的概率也大。也就是说,对应发光点、对应出射方向光越多,被采到的概率也越大。对应的pdf为:
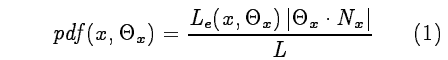
其中$L_{e}$为在x位置和Theta角度的发光大小,后面是Theta角度和法向量点乘的绝对值。下面的L是一个规约系数,目的是让整个pdf在定义域内的积分为1:
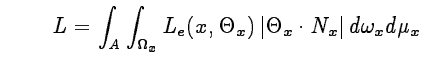
这里面有两层积分,内层是对球面上角度的emitter的积分,外层是对面积上x位置的积分。使用重要性采样的方法,可以采样出x和Theta。
对于眼睛顶点,生成$y_0$和$\Theta_{x_0}$:
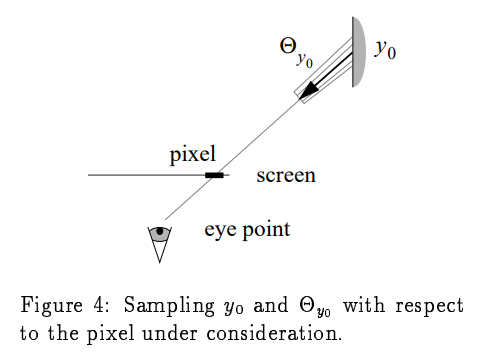
和上述方法相似,所使用的pdf如下:
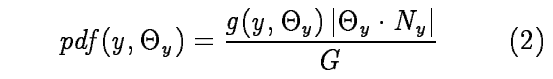
其中g函数表示y位置Theta方向上的光是否对我的pixel的flux有贡献,有则为0没有则为1。右面的点乘项同上,下面的G也是一个归一化系数,目的就是让pdf积分为1的:
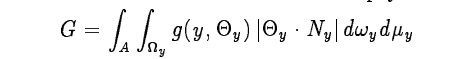
注意到这里的图和上面的图不太一样,对于光顶点,x可以是光源上面任意位置的任意方向,而这里面图上画的只是一系列射线延长线能到达pixel的点和方向的tuple。加上g函数非0即1,其本身不含有权重性质,这里的积分也就转化成那些眼顶点能到达的位置与方向的tuple,以方向和遇射点法线点乘的绝对值作为权重的积分。
总的来讲,这里sample的相当于眼点发出视锥中采样一条光路,不过这里的数学表示不是在视锥中对角度进行uniform采样,而是在视锥打到的面积上,对面积上的flux进行uniform采样。这样就保证了眼顶点的采样,对于反射面的flux是公平的(不论这个flux到底有咩有光路真正过来),保证采到这里的概率密度和实际上从这个位置来的光能量flux的占比相同就可以了。也就是,(我的理解)实际就是对满足条件(生成的射线经过pixel)的空间角进行uniform采样就可以了。
对于光顶点,生成$x_{i+1}$和$\Theta_{x_{i+1}}$:
经历完了上述步骤,初始$x_0$和$y_0$的方向和位置$\Theta_{x_{0}}$和$\Theta_{y_{0}}$就已经确定了,下一步就是如何sample得出两条光路下一步的出射方向$\Theta_{x_{i+1}}$和$\Theta_{y_{j+2}}$,从而进一步得出下一步$x_{i+1}$和$y_{j+2}$的位置。

如何生成$x_{i+1}$?只需要对$\Theta_{x_{i}}$对场景进行求交,得到的交点就是所求。
如何得到$\Theta_{x_{i+1}}$?这里需要对这个点进行采样,依据的是在这个点上的brdf:
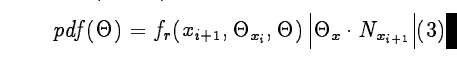
这里面没有对整个pdf进行归一化处理,在所有可能的角度上积分基本不可能为1,因此这个pdf被叫做亚临界概率密度函数(sub critical probability density function)。积分的实际值给出了继续随机行走的机会,这确保了随机行走终止。这种技术被称为俄罗斯轮盘赌。
对于视角顶点,生成$y_{i+1}$和$\Theta_{y_{j+1}}$:
和上面的方法类似。
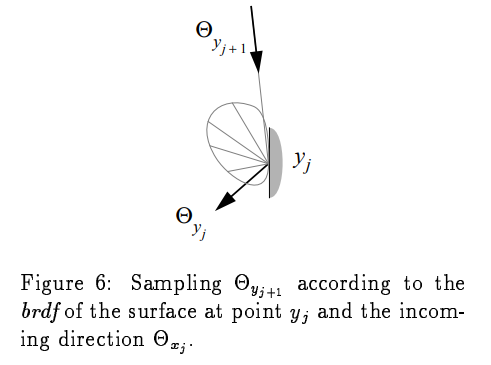
依据spdf:
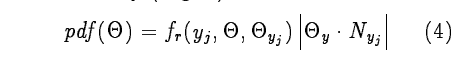
采样出出射方向$\Theta_{y_{j+1}}$,与场景相交后便可得到$y_{i+1}$。
这种随机行走(random walk)是彼此独立的,且方向的spdf可以通过重命名brdf的变量简单地实现。这个性质暗示着在初始化之后,两个随机行走都可以用一个相同的算法来实现。(论文的作者的意思是,这两种随机行走只需要调用一种函数就ok了)
Estimating the flux
上面说的是如何构成路径,接下来改计算每条路径上真正的光flux是多少了。知道了flux,也就是知道了pixel的实际颜色。其中flux中的每份能量都是由flux用一系列shadow ray加权求和算出来的
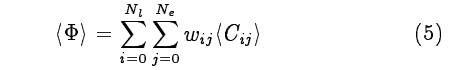
系数$\langle C_{i,j} \rangle$表示对光路上的i点的反射和在眼顶点上的j之间的flux。三种情况下C的计算方式也不同。
这里的C按我的理解,指的是
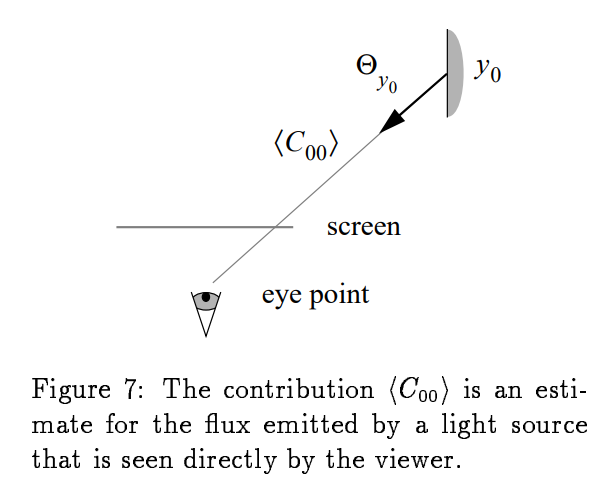
- $i=0,\ j=0\ : \langle C_{00} \rangle=G\times L_{e}(y_0,\Theta_{y_0})$
- 这里描述的是从眼睛直接收自来自光源的光的部分,因为y0就是光源采样出来的点。所以这个式子的意思就是说,用采出来的点的光强直接作为G这片面积内的flux。
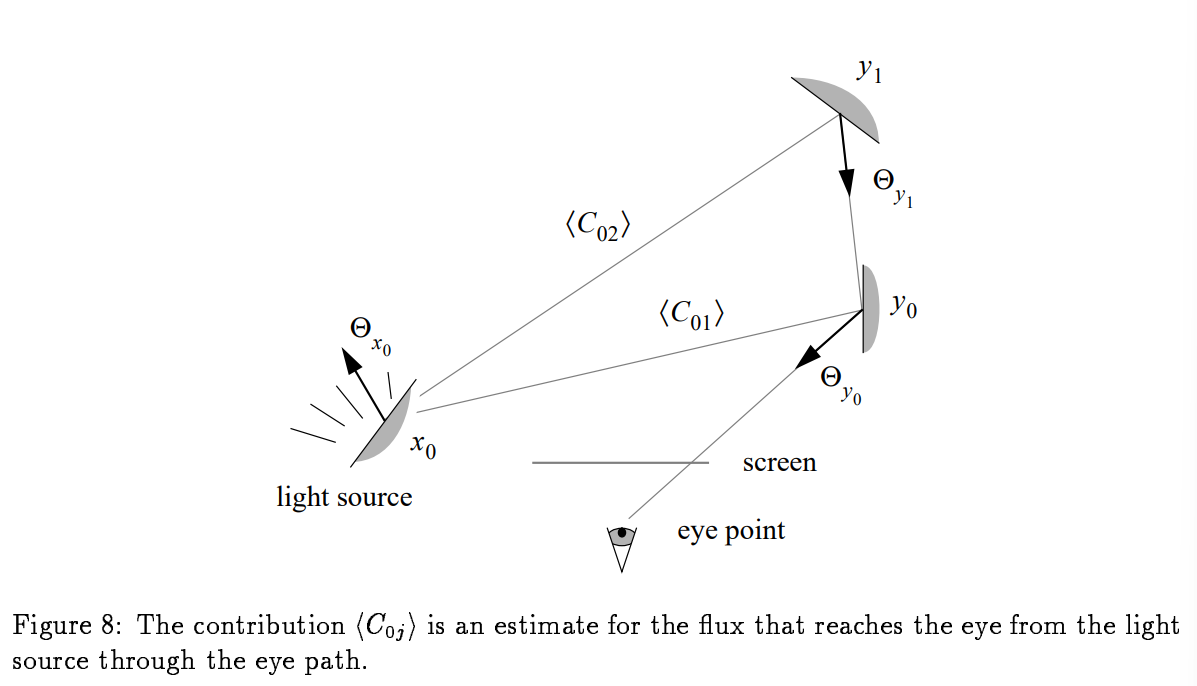
$i=0,j>0:\langle C_{0,j} \rangle=$
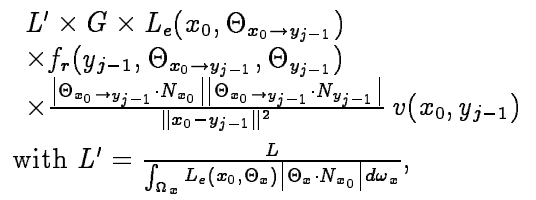
这项是对眼顶点到光源部分的衡量(fig. 8)
其中$\Theta_{x\rightarrow y}$是从点x到y的方向,v是可见性函数(x点和y点之间是否有其他物体遮挡)。这里求的其实是通过shadow ray来求出来的。
同时,对于经典的路径追踪,也是根据这个方法实现的。
公式分析:
- 首先明确L表示的是光源上所有点和方向的总flux,L’表示的是用总flux除以这个点方向角上的总flux。而Le除以L’下面的积分应该在单位上等价于brdf。
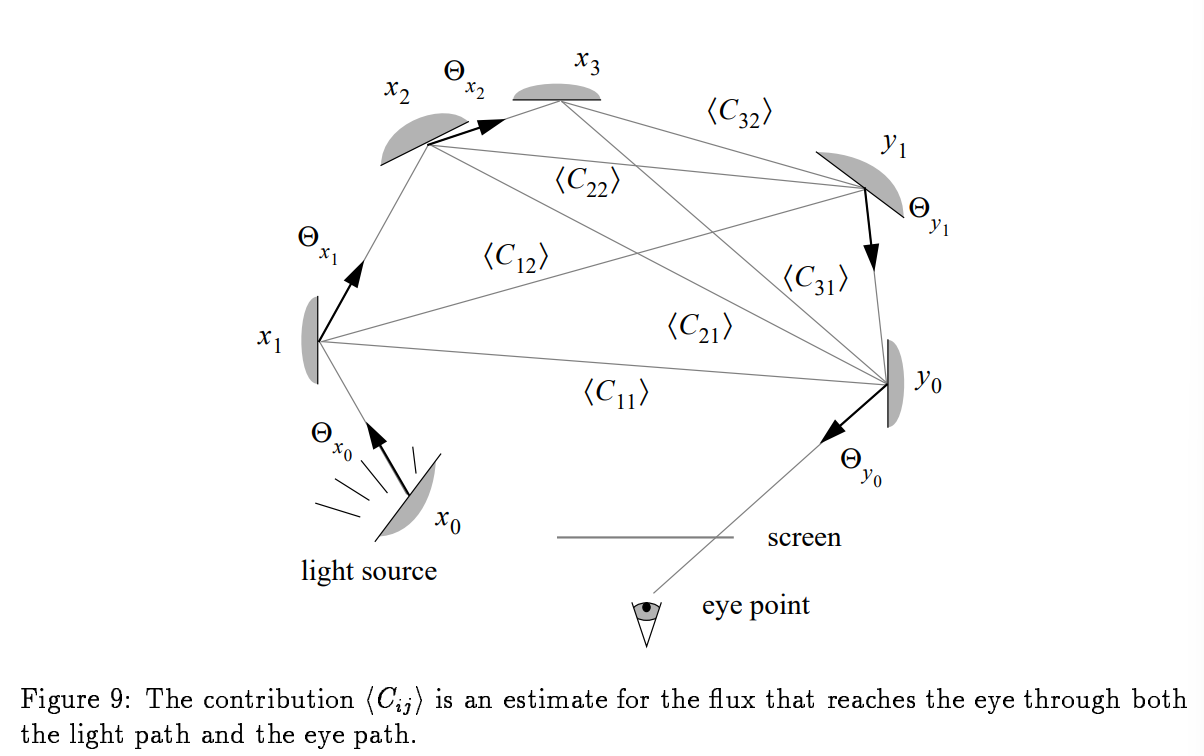
- $i>0,j>0:\langle C_{i,j} \rangle=$
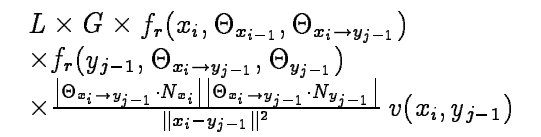
- 这部分就是关于视顶点和眼睛顶点的shadow ray的部分。
- 注意到这里的光顶点是直接是乘了L(也就是光源的总光强),没有弄每次光顶点上的损失。(这里的处理应该是在下面关于权重处实现的)、
- 而且,就算是得出了C,真正到达眼睛的颜色也是应该C每级每级递减才到达眼睛的。
Selecting the weights
上面讲的是C这部分怎么算,现在来好好捋捋前面的权重计算。
首先权重应该满足条件$\sum^{N}{i=0} w{i,N-i}=1 (N=0,1,…)$。这个条件yysy没理解。论文中说,这个条件可以通过理论推导出来,它物理意义是对通过1,2等等次折射到达眼定点的光通量的权重的集合加和为1。可以验证以下实例化产生了经典的路径跟踪算法:
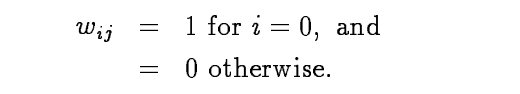
然而,此选择并没有完全使用采样过程的信息。以下备选方案使用两种粒子路径效果:
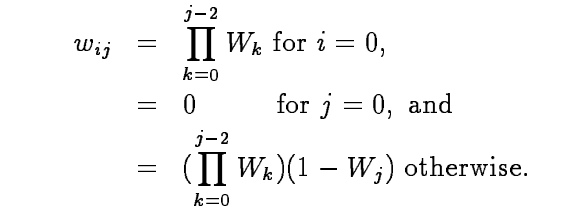
这里还有一系列自由度:$W_{j}(j=0,…,N_e-1)$。
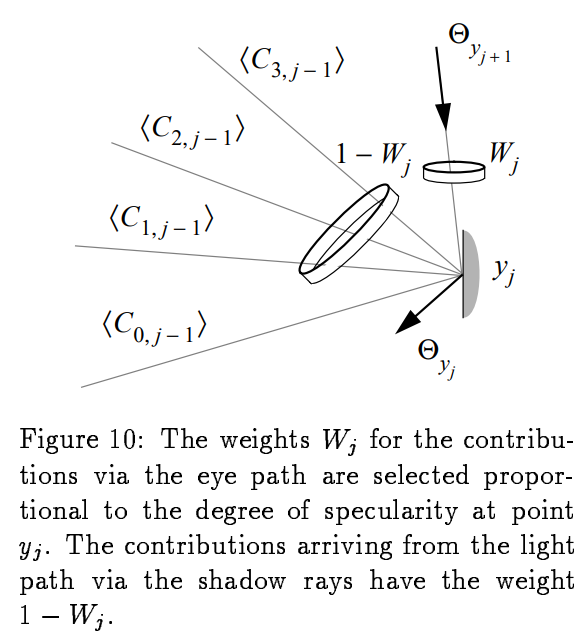
这种特定选择背后的思想是,在眼路径上的每个点处,对经由眼路径的其余部分和经由光路径的间接照明的估计进行加权。对于镜面反射曲面,人们更倾向于根据眼睛路径找到的估计值。对于漫反射表面,通过光路的贡献找到的估计更可能是重要的。因此,权重W被选择为与眼睛路径上的点y处的表面的镜面反射度的测量成比例。对于高度镜面反射的曲面,它将达到1,对于漫反射曲面,它会达到0。对实际场景的测试表明,这种技术大大提高了图像的质量,尤其是在渲染包含镜子的场景时。
Computing a secondary estimator
对光通量的原始股机器会有一个巨大的方差,这个效果会在图像上以随机噪声的形式明显地体现出来。就像所有蒙特卡罗方法一样,二次估计器是通过对单个像素的几个主要估计器的结果进行平均来计算的。如果N是原始的采样数量,平均结果的反差会以$\sqrt{N}$的速度下降。对于路径追踪N一般被设置为40到500之间,但是优化数量很大程度上依赖于场景的复杂度和所需的精度。一些启发式的自适应采样技巧经常被引入来找到一个介于计算量和最终质量的平衡。
IMPLEMENTATION
我们已经实现了所描述的双向路径跟踪算法。该程序是在IBM RS/6000-320上用编程语言C编写的。它基于公共领域射线追踪程序Rayshade的库例程。
brdfs是使用Phong model建模的,该模型经过了轻微修改,使其具有倒数和能量守恒性,允许对方程中的几个常数和pd/s进行分析计算。更复杂的模型通常需要数值技术。
几种优化的采样策略已经实施。重要性抽样和俄罗斯轮盘赌(这里的方法具体是怎么用的?glsl的path tracer是直接基于随机数和系数来选择是否毙掉这条光线)已经被应用,如前几段所述。此外,还使用了分层采样(?之前没提到过)。这项技术包括细分采样间隔,并从每个采样间隔中选择样本,而不是在整个采样间隔中随机选择所有样本。以这种方式选择的均匀样本可能会转换为非均匀样本,因此该技术很容易与重要性采样相结合
RESULT
这里不写了
CONCLUSION
机翻:
我们提出了双向路径跟踪作为一种新的基于物理渲染的蒙特卡罗算法。它可以在一个通用的理论框架中解释,其中现有的路径跟踪算法是一个特例。
- 与其他蒙特卡罗技术类似,该算法非常通用:它可以处理广泛的几何对象类和光学财产。漫反射照明效果-阴影、镜面反射和光泽反射和折射,以及均匀景深和运动模糊(如果需要)都可以正确模拟。抗锯齿是以一种自然的方式集成的。
- 实验表明,对于间接照明很重要的典型室内场景,该算法优于路径跟踪。
- 该方法不需要meshing,从而避免了所有相关的问题。也正因为如此,该方法只需要很少的内存。以只读方式访问场景描述
- 重要性抽样被广泛使用,极大地减少了方差。然而,在没有自适应采样的情况下,收敛相当缓慢。这在一定程度上是因为要为每个像素寻找精确的解,而不是有限元方法,在有限元方法中,最终的解大部分时间都在较大的表面积上插值。自适应和分层技术以及过滤应该有助于在未来的“oversolving”和“undersolving”之间找到适当的平衡。




