SPCBPT: Subspace-based Probabilistic Connections for Bidirectional Path Tracing

题目：对于双向路径追踪这个领域，基于子空间的概率链接。

第一印象：一种对于双向路径追踪的，针对于概率链接的优化，使用了子空间这个方法。

个人还是喜欢这种论文，相对于深度学习based的技术硬核太多了。

Abstraction

双向路径追踪可以通过选择合适的光线子路径的链接来进行加速优化。然而，现有的算法需要执行频率分布重建并且会有昂贵的开销（现有算法是什么？）。

我们提出了一种用于概率连接的新方法SPCBPT，该方法构造子路径空间中的光选择分布。我们的方法将子路径分为多个子空间，并将子路径保持在低差异的同一子空间中，其中可以通过基于子空间的两阶段采样方法来选择光子路径，即，首先对光子空间进行采样，然后对该子空间内的光子路径进行重新采样。基于子空间的分布不需要重建，并且以非常低的成本提供了有效的光选择。我们还提出了一种在光选择中考虑多重要性采样（MIS）项的方法，从而获得MIS感知分布，该分布可以最小化组合估计器的方差上限。先前的方法通常会省略这个MIS权重项。我们使用各种基准对我们的算法进行了评估，实验结果表明，与最先进的方法相比，我们的方法具有优越的性能，并且可以显著降低噪声。

1 Introduction

这里还是简要介绍了什么是双向路径追踪，我在读 BI-DIRECTIONAL PATH TRACING中给了对论文中的技术很详细的介绍，在论文阅读：Optimally Combining Sampling Techniques for Monte Carlo Rendering中给出了对多重重要性采样的介绍和说明。并在我们的HRRVC复现代码HRRVC/src/shaders/common/bidirectrace.glsl at main · SankHyan24/HRRVC · GitHub中实现了naive bidirectional path tracing的主要算法。

在经典的BDPT中，渲染器为每个跟踪的眼睛子路径生成（或选择）灯光子路径，然后连接这两个子路径以构建完整路径。经典的BDPT无法很好地处理这种光选择问题，因为连接的重要性采样较差，这导致效率非常低，尤其是在具有复杂可见性的场景中。

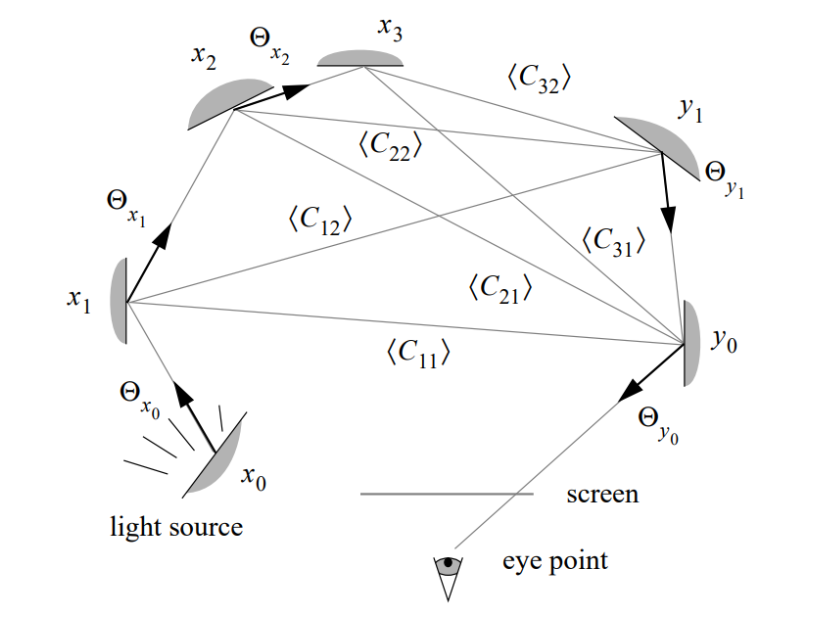
这里说明了BDPT的主要问题：算连接的时候的可见性检查很麻烦很费时间。如果我们重用光路径，这不但会产生一些因为相关性导致的方差增大的问题，而且还有个问题，就是在MIS中如何控制每部分的权重：

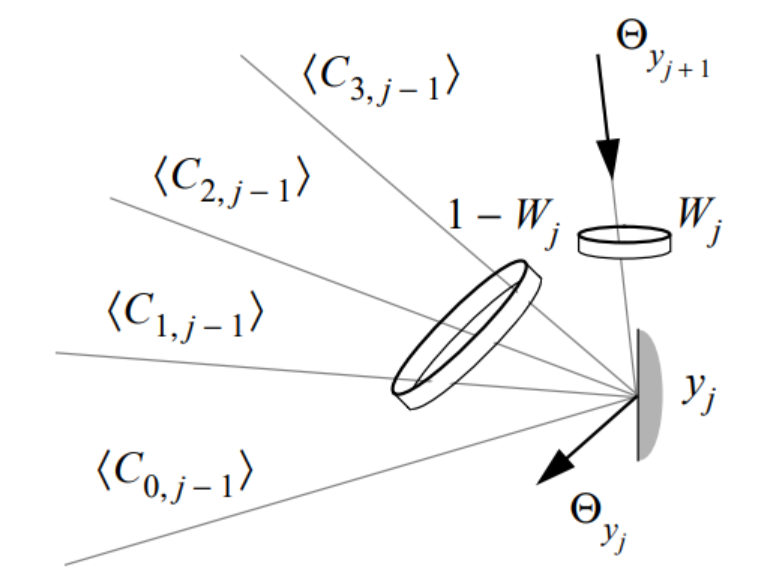
也就是这张图里面，这几个shadow ray的connection到底占比为多少。

Probabilistic connections for BDPT (PCBPT) [Popov et al. 2015] made an improvement by reusing multiple light sub-paths between different eye sub-paths and selecting the appropriate light sub-path regarding the constructed path contribution. Nabata et al. [2020a] proposed resampled importance sampling BDPT (RISBPT) by applying a resampling-aware MIS function to PCBPT and achieved significant noise reduction in various difficult scenarios. However, the candidate light sub-paths used for connection need frequent updates to achieve unbiasedness. As a result, PCBPT and RISBPT need millions of shadow rays to reconstruct the resampling probability mass function (PMF) stored in the cache points when updating the light sub-paths. This expensive overhead limits the number of candidate light sub-paths available and introduces visual artifacts in the early rendering stage. Furthermore, the sampling probabilities ignore multiple importance sampling weights, making PCBPT and RISBPT estimators difficult to achieve optimal.

这里介绍了SPBPT中的第一个P的来源“概率链接”技术。PCBPT（Probabilistic Connections for Bidirectional Path Tracing）算法大概流程：

这种技术重用了光路径，并用一种类似于“空间相似性”的方法，用一部分眼顶点的权重来近似周围所有眼顶点的权重，从而实现这种重用光路径的MIS方法。这种方法在比较大的场景中能比较显著地降噪，但是作者仍然认为这种做法在做PMF（也就是计算权重的概率密度函数）的时候开销太大了，并且限制了缓存光顶点的数量，并在渲染阶段的早期引入了artifact。并且概率采样忽略了mis weight这一步，让RISBPT和PCBPT更难实现最优。

之后就看作者怎么介绍自己的技术了：

In this paper, we present an approach to efficiently solve the light selection problem and eliminate the overhead of frequent PMF reconstruction. Different from the previous works that compute the PMF in a subpath-to-subpath manner, we present a novel sampling solution in the sub-path space. By grouping similar eye sub-paths and light sub-paths, we obtain a set of subspaces. Here, subspace is defined as a subset of the sub-path space, and sub-paths in the same subspace should be of low discrepancy and share sampling importance.

We generate the light sub-paths by first sampling the light subspace and then sampling the light sub-paths within the subspace, called two-stage sampling. Subspace sampling importance is consistent in the rendering and facilitates optimizing the estimator. We collect statistics in a preprocessing pass to determine the sampling importance in subspace. The optimal subspace sampling probability needs to consider multiple importance sampling. However, multiple importance sampling weights depend on the sampling probability. We solve this problem and show that the optimization of sampling importance that minimizes an upper bound of variance is convex, and then use stochastic gradient descent (SGD) to solve for the optimized light selection distribution. Therefore, we obtain an optimized MIS combined estimator based on the proposed MIS-aware light selection, which facilitates efficient sub-path sampling.

重点：基于PCBPT，提出了一种方法解决频繁重建PMF重建开销。

之前是使用PMF然后对PMF加权平均来求出PMF，这里的新方法，在子路径空间中提出了一种新的采样方法。通过堆相似的眼睛路径和光路径进行分组（group），获取一组子空间。

光路径部分的采样大概过程，两阶段：

第一阶段：采样一个光的子空间
第二阶段：在光的子空间里面采样出光路径。

每个光子在其子空间中都共享相同的权重，就是说给相似权重的光子分配到相同的子空间中。这样的话有利于优化estimator。

预处理过程中会cache一些数据用于确定数据在子空间的采样重要性权重。这里的对于权重估计是使用SGD（难道是神经网络了）来优化光选择分布的。

We illustrate the overview pipeline of our method in Figure 2. We highlight the novel modules in our algorithm based on the BDPT framework. The subspaces are first specified according to a classification function in the pre-trained stage (preprocessing). We then determine the MIS-aware light selection function by minimizing the variance upper bound. The selection function is used in runtime sub-paths sampling. In the runtime rendering stage, both light subpaths and eye sub-paths are binned into the subspaces, and then the two-stage sampling method is used to sample the subspace and sub-path for probabilistic connections. Finally, the full paths are constructed for an MIS combined estimator.

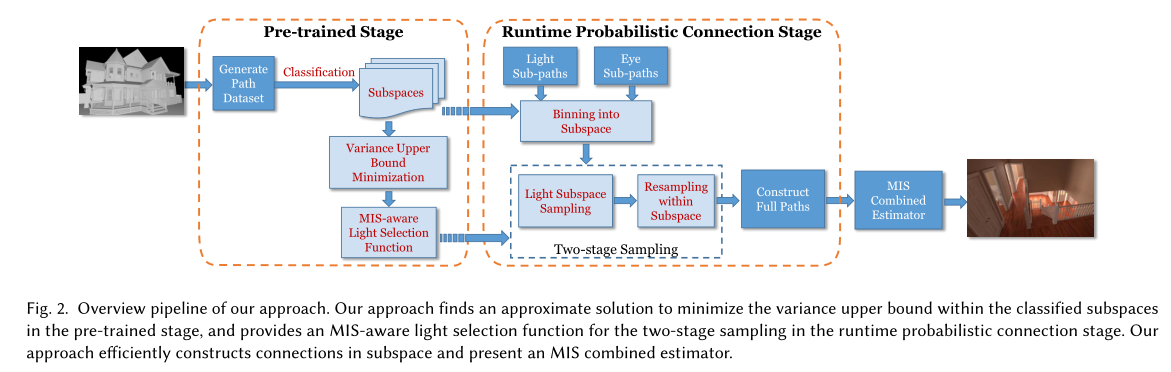
图2中说明了方法的概要流程：

在预训练阶段（预处理）中，首先根据分类函数指定子空间。
然后，通过最小化方差上界来确定MIS感知的光选择函数。选择函数用于运行时子路径采样。
在运行时渲染阶段，将光子路径和眼睛子路径合并到子空间中，然后使用两阶段采样方法对子空间和子路径进行采样，以实现概率连接。
最后，构造了MIS组合估计器的全路径。

这部分主要对每段讲了啥技术简单说一下，不多详细赘述。

The key of BDPT is to establish the connections between the eye vertices (i.e., eye sub-path) and the light vertices (i.e., light subpath) [Pajot et al. 2011; Popov et al. 2015; Walter et al. 2012]. Davidovič et al. proposed light vertex cache BDPT (LVCBPT), which uses light vertex cache to store and resample light sub-paths

这里主要说明光顶点缓存技术。

Importance sampling between bidirectional probabilistic path connections is a key factor affecting efficiency [Georgiev et al. 2012b]. Popov et al. [2015] proposed PCBPT to reuse multiple light subpaths. It samples the connections between the eye sub-path and a few light sub-paths regarding full path contribution. PCBPT’s importance sampling is a resampling method [Talbot et al. 2005]. After that, Nabata et al. [2020a] proposed RISBPT, which provides MIS weighting functions for PCBPT. In addition to PCBPT, Tokuyoshi and Harada [2019] proposed a hierarchical Russian roulette (HRR) scheme that use BVH to construct connections between eye vertex and light vertices within the BRDF scattering range. Matrix BDPT reorders sub-paths and builds a matrix from light sub-paths and eye sub-paths to improve connection sampling [Chaitanya et al. 2018]. Bitterli et al. [2020] used resampling of direct lighting and achieves significant improvement in real-time.

这里主要是讲对于光顶点缓存之后，该如何进行链接（PCBPT）和优化（HRR）的。这里@到了我们在图形学研究进展大作业里面复现的层次化俄罗斯轮盘赌。

Many-light methods [Keller 1997; Krivanek et al. 2014] also study the connections between eye sub-path and multiple light sub-paths. Many algorithms select a small portion of the light vertices to connect to improve efficiency [Georgiev et al. 2012b; Hašan and Pellacini 2007; Walter et al. 2006, 2005]. Walter et al. [2012] proposed bidirectional lightcut and introduced MIS into the many-light method. Previous works also find that light selection efficiency can be improved by clustering light sources [Ou and Pellacini 2011; Wang et al. 2021; Wu and Chuang 2013]. Compared to the many-light method, our algorithm focuses on those BDPT scenarios that require special handling of clustering and multiple importance sampling.

这里提及到的是many-light method以及相关方法。我没具体阅读过论文，查资料的结论是：多光绘制算法把递归地求解绘制方程这一复杂的问题近似为计算大量虚拟点光源的直接光照这一相对简单的问题。大概就是把次级光源当成虚拟点光源，然后light cuts方法就是把多个贡献小的光源近似为一个更亮的表征光源。不过作者说了相对于这些工作，他们的工作更倾向于其他方面。

Two-stage RISBPT [Nabata et al. 2020b] combines RISBPT with lightcuts and uses lightcuts to sample candidate sub-paths that are likely to contribute highly to the current eye sub-path. However, visibility is ignored when candidates are sampled from the light tree, and the reconstruction of light tree can be expensive. Furthermore, the target probability density function (PDF) of the two-stage algorithm omits the MIS weight, which makes it difficult to obtain a sampling distribution that minimizes the global variance.

两阶段RISBPT及其优缺点。

Path guiding methods can importance sample paths adaptively according to the scene’s illumination distribution [Jensen 1996; Lafortune and Willems 1999]. Vorba et al. [2014] proposed a Gaussian mixture model for path guiding. Müller et al. [2017] proposed an adaptive spatio-directional tree (SD-tree) to represent the incident radiance field based on the spatial binary tree structure of the scene. Other extensions of path guiding include product path guiding [Herholz et al. 2016], using linearly transformed cosines [Diolatzis et al. 2020], using neural networks [Müller et al. 2019, 2020], or guiding the sampling direction in the primary space [Guo et al. 2018]. Variance-aware path guiding [Rath et al. 2020] guides the tracing process in a distribution that can minimize variance. This inspires us to deal with the MIS-aware distribution. MCMC methods importance sample a new path by perturbing the existing one for scenes with highly complex visibility [Jakob and Marschner 2012; Veach and Guibas 1997]. It can also be applied to tracing valuable light sub-paths, but the sampled path may be stuck in a local path space.

自适应对路径进行采样的方法，论文没读过，看起来都是强调一个自适应。

3 Preliminaries

很多论文里面都有这部分，就是介绍背景知识并引出自己技术的。

3.1 Resampled Importance Sampling

这里放原文会因为数学符号无法识别而出乱码，就不放了。

重采样重要性采样（RIS）是一种可以生成和任何目标分布类似分布的采样技术。对于目标分布$q$，RIS先从PDF $p$中生成一系列候选样本M。然后样本被从候选的里面选择出来按照一个比例也就是$q/p$，如果候选集和M充分大的话，RIS可以生成近似的目标分布。

3.2 Bidirectional Path Tracing (BDPT)

对于每个pixel的衡量值$I$的积分公式：

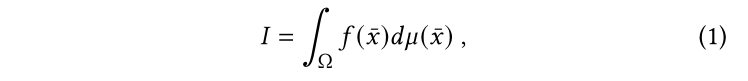
这里的符号比较特别。

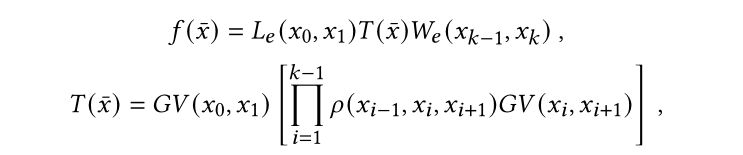
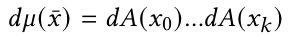
$L_e$是物体从x0到x1的radiance散射，$W_e$是pixel sensitivity（具体是啥我也不知道，不过看这个渲染方程，它应该就是我们常用的cosine项了），$\rho$是BSDF（可以理解成高级版的BRDF，包括了折射部分），$GV$是一个几何项，也就是是否可见（visibility）。

之后就是MIS。

上图，对于BDPT，由于有很多种的采样策略，比如说长度为3的路径就有很多很多种采样方法，所以需要一种方法把这些策略加权合到一起，也就是MIS。

n种策略的MIS方法如下：

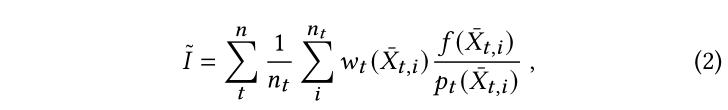
这里的nt是每种策略的采样数量，w就是“主角”——权重。f是值，pt是通过这个策略算出来的pdf的概率。

为了要实现unbias，需要对于每种才出的路径的权重和为1，特别的pdf为0的时候weight也需要是0。目前这些系列的mis方法中降低方差比较好的就是balance heuristic：

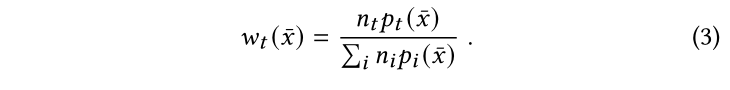
3.3 Light Sub-paths Reuse and Probabilistic Connections

BDPT为每个像素追踪来自相机的眼睛子路径和来自光源的光子路径。LVCBPT通过在不同的眼睛子路径中重用多个光子路径来扩展BDPT。

LVCBPT迭代地估计像素强度。在每次渲染迭代中，LVCBPT在一次过程中跟踪多个灯光子路径，并将灯光顶点（即灯光子路径的前缀）存储在称为“灯光顶点缓存”（LVC）的缓存中。LVC中的每个前缀子路径可以被视为单独的子路径。然后，从LVC中随机选择光子路径，以与每个眼睛子路径连接，并最终构建完整路径。

从LVCsample一条光的子路径可以被认为是用一种重新采样的方法从一个子路径空间中采样，即将光子路径的$p(\bar{y})$作为目标分布。PCBPT使用一种对于cached的光的子路径进行mis，并且把f的分布分成fzfyz和fy三部分：

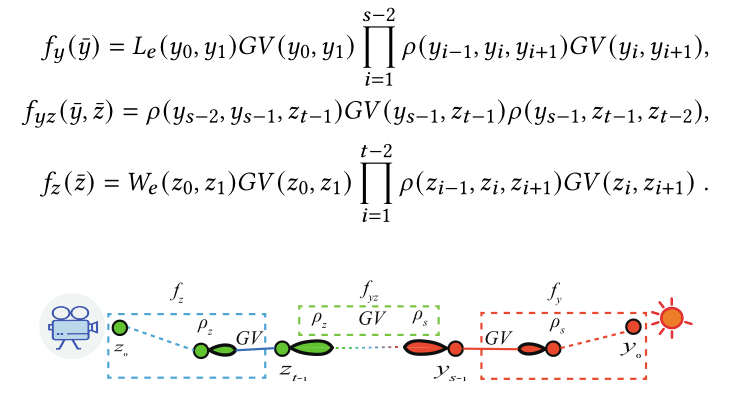
这里的fz在连接中被共享，所以可以被忽略掉，所以PCBPT的概率应该使用$p(\bar{y}|\bar{z})=f_{yz}(\bar{y},\bar{z})f_y(\bar{y})$作为对于光路径重新sample的目标分布，并据此构成PMF记录。相邻的眼睛子路径可以共享他们的PMF记录，避免了重复的对PMF的构建。PCBPT的MIS weighting function不能解决resampling引入的PDF的方差，RISBPT被提出来解决这个问题，通过使用resample-aware weighting functions，从而大大提升了渲染质量。

然而，RISBPT并不涉及目标分布中的MIS。很难解决MIS感知的采样分布，因为MIS还需要采样分布来确定权重。因此，RISBPT估计器可以进一步优化。此外，RISBPT需要一个额外的可见性测试来构建PMF记录，并且这种计算开销将减少给定时间预算下可能的迭代次数，并限制光子路径的数量M 用于重新采样。RIS的性能在很大程度上取决于候选数量M. 在能见度较低的场景中M RISBPT的不足以提供接近目标分布的采样，并且效率较低。

4 Overview

这里作者终于要开始说他自己的东西了。一般这部分都是放在第二节后面：

算法遵循与LVCBPT和PCBPT相同的概率连接方案。因此，我们的目标是对候选光子路径进行重新采样，并为每个眼睛子路径选择合适的光子路径，以有效地构建连接。用于重新采样的目标PDF应易于评估渲染效率，并且重新采样分布应尽可能避免重建。

这个方法的关键是将子路径分类为多个子空间，从而将子路径保持在低差异的同一子空间中。然后，我们可以通过考虑多重重要性采样来确定最优子空间连接概率。

相似光路径分组放在一起，当成相似的PMF类似的方式对待。

作者的方法：

我们首先建立了基于子空间的采样和概率连接的理论基础（第5节）。我们从概率连接的最优分布开始，推导了基于子空间的光选择函数的公式，该函数可用于近似最优分布。
接下来，关键问题是找到一个有效的解决方案，以实现实际的子路径采样（第6节）。通过将近似分布设置为目标PDF，我们提出了一种基于子空间的两阶段采样方法和估计器（第6.1节）。MIS需要每个采样策略的采样密度来计算MIS权重，而采样密度取决于光选择的分布。因此，我们提出了考虑子空间采样的MIS加权函数（第6.2节）。我们还涉及MIS加权函数，以使子空间中的光选择最优。我们证明了关于子空间采样分布，估计方差上界的最小化是凸的，这导致了MIS感知的采样分布，并且可以通过随机梯度下降（SGD）来解决（第6.3节）。这也有助于解决MIS加权函数和采样分布之间的循环依赖问题。子空间的分类影响性能.
最后，第7节介绍了子空间采样的一些技术细节。我们运行预处理过程并跟踪路径数据集D（第7.1节）。基于该数据集，我们对子空间进行分类，并构建用于快速子空间装箱的决策树（第7.2节）。通过最小化该数据集中路径方差的上限，可以获得基于子空间的MIS感知采样分布（第7.3节）。此外，我们采用交叉迭代光子路径复用来进一步提高效率（第7.4节）。

5 Subspace-based Probabilistic Connections: Principle

这一节先建个但是子空间的光选择函数，是后面采样方法的基础。

5.1 Optimal Distribution of Probabilistic Connections

首先考虑概率连接算法中的基本连接原理，如LVCBPT和PCBPT。从相机跟踪眼睛子路径，并将其与从候选光子路径重新采样的光子路径连接，并估计每个完整路径的加权贡献。采样策略由眼睛子路径的顶点数量来识别；策略t 是指通过连接的眼睛子路径来生成完整路径t 具有任意长度的光子路径的顶点。因此，像素测量t 在等式1中可以重新表述为:

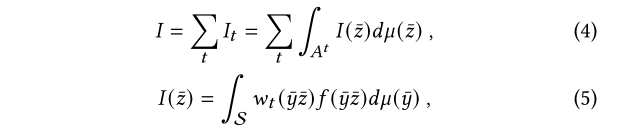
这里的$A^t$是一个在场景表面A上的t维笛卡尔内积，$S = \cup_tA^t$狮子路径的子空间。t表示眼子路径$\bar{z}$的节点数量，用来辨识采样策略的。

蒙特卡洛估计被用来估计$I(\bar{z})$，估计$I(\bar{z})$的最优的分布$p^*(\bar{y}|\bar{z})$应该满足：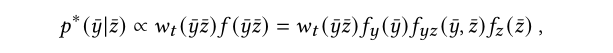

因为这里面fz是与ybar独立的（前面介绍PCBPT的时候说了），所以可以被忽略，因此：

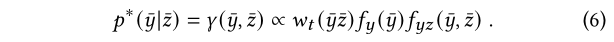
这里定义最优的光线选择函数$\gamma(\bar{y},\bar{z})$，这是一个$\mathcal{S}\times \mathcal{S} \rightarrow \mathcal{R}$的函数，返回的是最优的采样的概率密度。对于任何给定的z都能得到y在z下的边缘最优分布。

现在问题来到了这里：怎么求这个gamma？

5.2 Approximate Formulation of $\gamma$

简单的连续函数其实不好定义这个gamma。作者用了一种近似地离散的方法，并引入了子空间，来获取一个对于$\mathcal{S}$的分段的表示。通过将S分成一个个子空间，作者近似估算出gamma对于每个子空间对子空间对的值。

也就是说：把定义域分片离散化，最后得到一个结果有限的值离散的函数。

形式化地引入子空间分类函数$\kappa:\mathcal{S}\rightarrow Z$，Z是每个子空间的ID。由于光路径和眼睛路径的分布不同，因此分类函数也被分为$\kappa_\mathcal{L}$与$\kappa_\mathcal{E}$，于是乎：

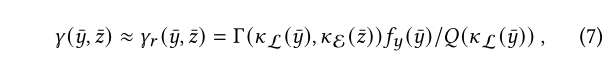
$\Gamma$是满足$\sum_i\Gamma(i,j)=1$对于任何$j\ge0$的左随机矩阵（left stochastic matrix）。$\mathcal{Q}$是归一化项：

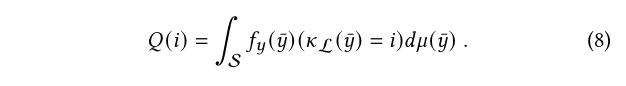
来确保对于对于每个zbar都成立，因为$\gamma_r(\bar{y}|\bar{z})$是概率密度函数。

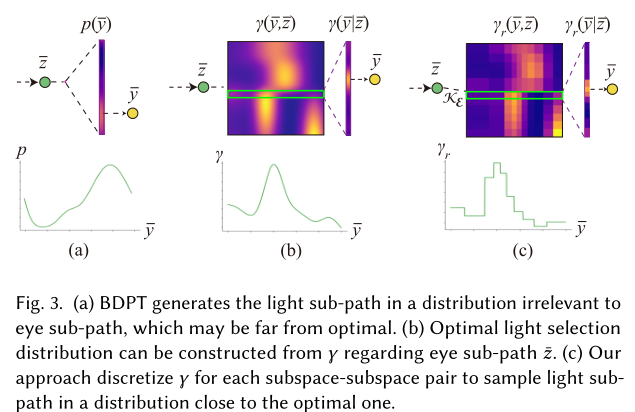
上面这张图就是对离散化思想的一种形象描述。

6 Subspace-based Probabilistic Connections: Method

具体来讲，三个内容：

两阶段采样方法，有效地根据概率密度函数为estimator提供样本
MIS的权重函数，以及优化矩阵$\Gamma$的方法，据此可以最小化方差上界
将空间划分为子空间，并且使得子空间中差异较小

6.1 Two-stage Sampling and Estimator for $\gamma_r$

作者使用的一种类似于LVCBPT的方法，对于每个渲染的iteration，从光源以PDF$p(\bar{y})$trace M 子路径，将每一个前置子路径作为一个独立的候选路径Ybar，并构建LVC（光顶点缓存）。

不同于LVCBPT：构建的LVC对于每个子路径都是独立构建的而不是把整个路径空间都放进去。每个光子路径Ybar被放到所属子空间的LVC中。

对于每个从照相机里面trace出来的眼路径Zbar，resample分为两步：

Stage 1: 先从子空间里面抽样，根据pmf 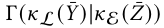来得到是哪个子空间。
Stage 2: 再从子空间里面根据目标pdf分布的比例采样出光的子路径。

stage2的resampling的PMF是：

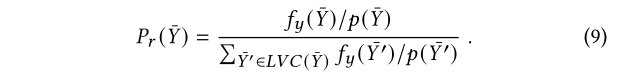
Q作为gamma_r的归一化项，在同一子空间中相同所以在上式中消掉了。

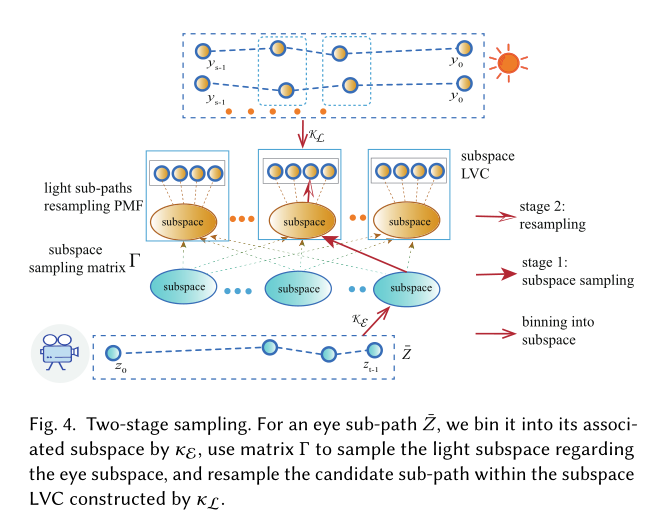
上图描述了LVC过程和子空间采样的流程。实际上考虑到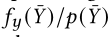和眼路径Zbar是不相关的，所以构造的PMF只需要每次iteration中构建一次并且不需要额外的可见性测试。因此，只有一小部分的计算是必要的。

作者的estimator是这样的：

6.2 MIS Function for Subspace-Based Connection

概率连接会改变完整路径的采样PDF。对于光子路径ybar的选择，是取决于gamma_r的。因此对于策略t，目标pdf：

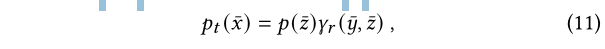
传统BDPT可以高效地解决t=1的是偶，因此t=0,1,k+1的策略可以同样地被传统BDPT解决。作者的方法只针对于策略t在2,3,…,k的情况，并且这些情况下的pt都会通过上面图的方程算出来。

mis的话，还是使用balance heuristic：

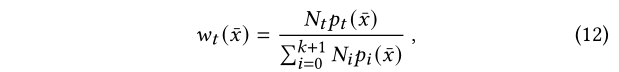
字母N代表的采样次数，就是平常的balance heuristic形式，略去不表。更多的关于Nt怎么选择来减少方差的讨论可以在 Grittmann et al. [2021]; Popov et al. [2015].中找到（找时间去看看）

6.3 MIS-Aware $\Gamma$ Minimizing Upper Bound of Variance

一般来说，在光选择的分布中MIS通常就被忽略了，所以Gamma可以根据子空间之间的全路径贡献来评估为：

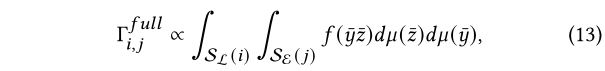
这里的$\mathcal{S}()$特指那个子空间。

$\Gamma^{full}$不是优化的，因为没有MIS。一个直接的恢复MIS项并且加入MIS-ware Gamma的方法就是对贡献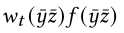按照权重进行积分。然而这个问题是不可能的循环依赖问题。

为了处理这个循环依赖，作者分析了采样产生的方差，然后提出了一个MIS感知Γ的解，该解最小化了方差的上界，并证明了最小化是一个凸优化问题。

什么是凸优化问题这里我都没弄明白，前面的区域以后再来探索吧。

6.4 Classification Function

分类函数负责将空间S划分成一系列子空间。直接光照对于渲染是很重要的，并且在以前的工作中，光源的划分和聚类已经得到了广泛的讨论。因此휅函数$\kappa$用于可以容易地构造光源的子路径。然而，对于一般子路径，S是覆盖任意维度的空间的并集。子空间的数量通常是有限的，因为$O(N^2)$ 子空间采样矩阵Γ的开销。通过简单的分割来划分子路径空间S是不切实际的。因此，我们采用质心距离方案来定义分类函数。

使用质心子路径集${\bar{C_i}}$ 表示子空间中心，距离函数d 为了评估子路径之间的距离，子路径的子空间取决于其最近的质心子路径。

因此定义一个之心函数：

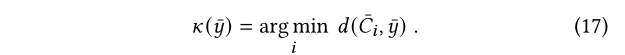
也就是说离哪个质心近就会被划分到一起。这里确定质心的方法很像kmeans那种方法，质心会被重新更新。现在来讨论d

作者认为，fyz取决于子路径最后一个顶点的位置、法线和入射方向距离，因此d函数是被这样定义的：

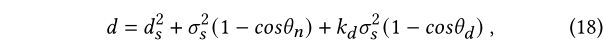
其中ds是空间距离spatial distance，$\theta_n$是normals之间的夹角，$\theta_d$是两个入射点的角度。sigma_s是对空间尺度的measures，作者trace一系列完整路径，并且通过顶点之间的空间差别来决定sigma_s。kd用来衡量入射角方向上的差异。事实上kd被设定为一个很小的值，因为大多数情况下位置和法向量在d中应该扮演更加重要的位置。

总的来说，这个过程就是d的能量优化，而这个d好不好完全决定了最后渲染的效果。

基于质心的算法是expensive的，作者在这里用的是近似方法决策树来实现这个算法。

7 Technical Details And Algorithm

8 Experiments and Results

这两部分主要是对代码实现trick的一些解释和最终实验结果的分析。在此略去不表。

9 Conclusion, Limitaion, and Future Work

这部分是作者的总结，直接上翻译：

基于概率连接的子空间公式，我们提出了一种可行的基于子空间的方法，用于从大量候选光子路径中进行重要性采样。通过首先对光子空间进行采样，然后从光子空间对光子路径进行重新采样，我们的算法可以显著提高复杂场景中的渲染质量，而计算开销很小。我们对概率连接的工作对生成子路径的方式没有具体的限制。因此，我们的算法可以使用任何特定的光路生成方法，如路径引导（见第8.4节）。

在预处理阶段，我们的方法需要大量的路径来训练近似函数훾푟 . 然而，在能见度很高的场景中，即使对这些路径进行预处理以进行训练仍然是一个挑战。像MCMC[Veach和Guibas 1997]这样的自适应采样策略可能是这个问题的解决方案，需要进一步研究。在线培训策略可以替代解决功能훾푟 而不是预先培训，值得未来调查。我们提出的MIS感知Γ是基于平衡启发式的。我们的方法与其他MIS加权函数（如相关性感知MIS）的组合【Grittmann等人，2021】应进一步讨论。在本文中，훾 通过将S划分为不同的子空间来近似地评估。然而，光子空间划分的方式可能不适用于所有的眼睛子空间。从粗到细的划分可以提供更好的近似，但这种划分的采样和MIS计算需要进一步研究.

由于BDPT的限制，一些困难的路径配置仍然很难处理，例如，高光泽材料（见图15）或由完美镜面反射引起的焦散。我们的方法也不能很好地处理这种类型的场景。通常，路径引导是必要的，以帮助平滑地渲染有光泽的曲面。VCM/UPS框架[Georgiev等人2012a；Hachisuka等人2012]提供了将BDPT与PPM相结合来解决焦散路径的方法，也可以与我们的算法相结合。最近关于PPM的工作通过减少光子收集的半径取得了很大的改进[Hachisuka和Jensen 2009；Lin等人2020]并将光子的形式扩展到高维光子表面[Deng等人2019]。将我们的算法与这些方法相结合以进一步提高效率将是一项有趣的未来工作。

我的总结：

总的来说，是一种对PCBPT有所创新的方法。PCBPT是将相邻的点作为PMF的依据，而SPCBPT做的更为彻底，直接划分成子空间，再在子空间中进行采样。结合了人工智能，未来这种子空间划分也许能通过ai来更好地划分，而不是只是根据自己通过heuristic定义的距离函数来进行质心距离划分了。