Progressive Photon Mapping 论文阅读 + Falcor 实践
Progressive Photon Mapping 论文阅读 + Falcor 实践
Abstract & 1 Introduction & 2 Related Work & 3 Overview的一部分 太长不看
光线追踪系列技术很大的一个难点在于很多采样是没用的采样,也就是采不到光上面,导致了发射了大量光线但实际上对最终结果做出实际贡献的很少。路径追踪提供的额外的对光源采样的采样方式让采样相对更加高效率,但是对于场景中间接光源比较多的情况下,路径追踪的效果也并不是很好。于是有了双向路径追踪,相当于扩展了光源的概念,让简介光照的点也成了抽象光源,但是慢也成了限制他的最大因素。MLT方法也是从有效的采样出发,尽量继续生成“有效”采样,达到相同时间下更好的收敛性。
但是种种以上都不能很好地解决caustic问题,也就是玻璃类似的材质下折射、反射形成的独特的形状。原因是(当时历史下),现有的无偏MC方法对这种SDS(Specular-Diffuse-Specular)路径的采样概率不高。在这种情况下,上述方法如PT是收敛的极慢,BDPT有所改善,但是对于光子映射系列方法,其效果特别好。
原理是从光源出发,射出一系列光子,作为一个photon map存储下来,在下一个阶段,也就是正常的eye trace阶段,借用之前photon map的信息作为估计hit point所在位置radiance的依据。
估计radiance有很多种方法,比如说统计每个hit point周围单位球附近光子的数量和能量,或者根据hit point最近k个光子的能量。但这些方法都会有一个问题,就是存在bias,将渲染方程中,积分项中的$\frac{\mathrm{d}E}{\mathrm{d}A}$简化成了$\frac{\Delta E}{\Delta A}$。但是只有当光子数量N趋近于无穷大的时候,上述两者才会相同。总之方法并不是无偏的,但是是consistent的。
3 Overview
光子映射本来挺好的,但是问题也很明显,就是最终效果依赖于photon map的大小。限制PT和BDPT效果的只有时间,最多区别也就是快慢,但是classic photon mapping的限制因素还有空间——光子图的大小,光子图大小限制了估计的准确性。于是就有了progressive photon mapping,相对来说更成熟更加实用一点,因此falcor的光子映射算法实现我也暂时选择使用ppm。
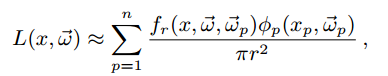
公式1,pm的基本公式,也是光子估算的原理,这里用的是相邻n的方法选取附近的光子。
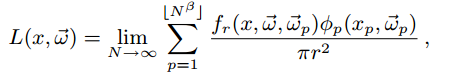
公式2,也就是之前说的光子数量无穷大的情况。
3.1 Progressive Photon Mapping
PPM把Classic PM的两个pass调换了一下,也就是先ray trace pass然后再photon tracing pass,这步photon Tracing可以根据想要的结果延长想要的时间,也就是进行多次sample直到满意那种。
Ray Tracing Pass:
从眼睛出发,每个像素发射光线。和光追差不多,区别在于停止条件,以及并不对光源采样。光线从眼睛射出去之后,会在diffuse的表面上停止,或者在specular的折射/反射的表面上继续折射反射。对于反射太多的场景,可以采用RR来限制迭代次数。对于每个像素点,都需要获取hitpoint停止后的值。
hitpoint在行进过程中,需要维护以下几项:(这里我和论文里的不一样,因为要适配特定渲染器,但是总体上思路没有任何区别)
struct hitpoint{ |
Photon Tracing Passes:
在我的想法和实现中,这步应该分为生成光子和统计radiance两部分。论文中的方法是,每次生成一系列光子,然后统计贡献之后扔掉光子,再生成一系列光子这样子循环往复。但是如果是写成shader的话,尤其是falcor的render pass,不太会怎么让生成光子和光子统计这两步能够循环执行。可能只能让这个整个render pass跑过一遍之后在下一遍的时候保留上一遍的值。
具体的描述在下一章节。主要翻译原文就不按自己理解说了。
4 Progressive Radiance Estimate
首先是原理。
传统的局部光子密度估计公式:
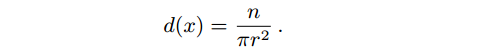
就是说,这是在一个点附近r的大圈圈里面找到多少个光子。但是如果我再生成一个Photon map,用相同的disc(也就是相同半径下),可能会得到不同的结果n’,对应不同的结果d’。
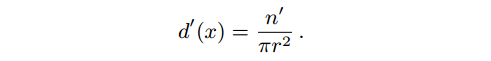
一般来讲,我们整合这两种方法的办法就是给n和n’去取一个平均值,然后得到更“精准”的预测结果。然而这种方法得到的结果并不会提升估算的精度,最后的结果不出意料会很模糊,因为r总是一个定值。总之这个方法更多的光子图并不会给渲染结果提供更多的细节。PPM相比之下的方法随着光子图的增多,会逐步地把r缩小,从而达到图片细节精度上的提升。
4.1 Radius Reduction
hitpoint的坐标点记为x。为了达到更好的估计结果,我们的目的就是如何随着光子pass的增加,增加搜索范围中的光子数量N(x),以及逐步缩小hitpoint所对应的光子搜索半径R(x)。这是达成整篇文章的最终目的的手段。
如果额外执行一个光子pass,并将新落入R(x)中的光子数量记为M(x),则有新的估计结果:
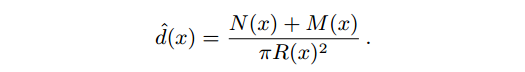
算法下一步是把半径R(x)减小dR(x)。如果我们估算R(x)内光子密度恒定,则可以通过R_hat(x)=R(x)-dR(x)估算新的光子数量:
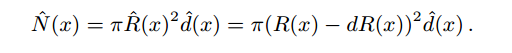
为了保证就算R减小了,每次pass区域内的N能增加,用一个参数alpha来控制N_hat:
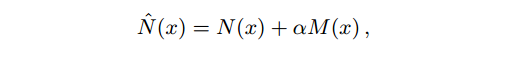
联立上面三个方程,然后推出dR(x)的值。
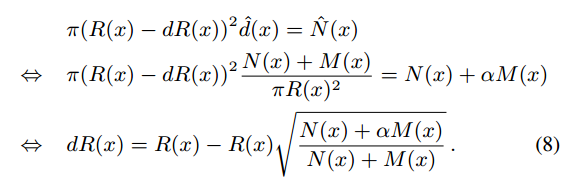
最后得出R_hat和alpha之间的关系:
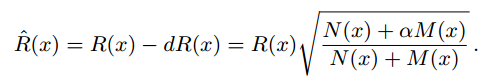
请注意,该方程是针对每个hitpoint独立求解的。
评价一下。首先上面这个方程的前提条件是:N(x)是趋向于均匀分布在disc里面的。对于充分小的disc,这种说法并没有问题,问题就怕disc还很大的时候,这个光子数量都集中在disc的外围,圆心附近很少。用alpha减少R(x)的面积也会对应把N(x)也减少了。总之这个方程成立的前提是N(x)~R^2(x)。
4.2 Flux Correction
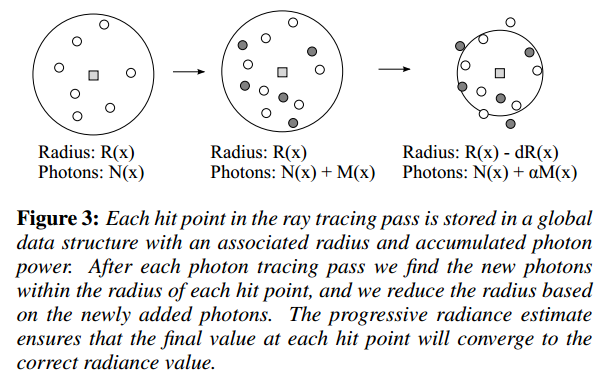
之所以要修正flux,是因为你减少了半径,原先被你包含进radiance的光子有的也被你踢出去了。如下图第三个步骤中的白色圆点。这个hitpoint是只维护disc中光子的总radiance,不会管具体哪些光子在里面。所以这里也需要一些假设和近似。
之前pass得到的flux:
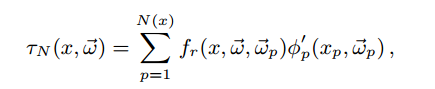
新增pass的那部分光子的flux:
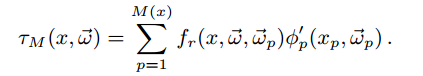
因为两个R变了,所以这两个flux不能简单地相加。还是之前的假设,光子在disc里面密度一致(均匀分布),则有新的flux:
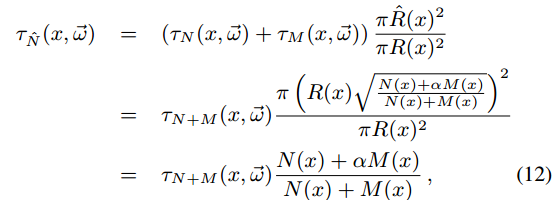
4.3 Radiance Evaluation
为了评估辐射率,我们还需要知道发射光子的总数,以便标准化τ,
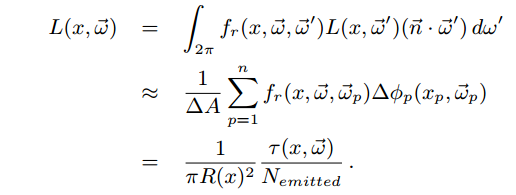
Nemitted就是你发射的光子的总数目。
文章还说了一些关于consistent的说明。




